以矩阵乘为例的BANG C编程实验
前言
整篇文章首先介绍BANG C开发的整个流程,以具体例子(矩阵乘)来详细介绍BANG C的开发和优化,最后展示每一步优化的性能情况。
一、概述
BANG C是寒武纪针对MLU硬件提出的专用编程语言,它由C语言扩展而来。BANG C采用异构编程,一个完整的BANG C程序在HOST端和MLU端分别进行编程、编译,最后链接成一个可执行程序。
HOST端使用C/C++语言进行编写,调用寒武纪的CNRT接口执行控制部分和串行任务;MLU端使用BANG C编写,执行计算部分和并行任务。
用户在HOST端输入数据,做一定的处理后,通过Kernel启动函数将相应输入数据传给MLU端,MLU端进行计算,再将计算结果拷回HOST端。
接下来就以矩阵乘的程序示例详细介绍BANG C的编程过程,以及如何利用MLU硬件架构优势去优化。编程技巧和优化的部分涵盖了片上数据调度,计算向量化操作及相应的数据对齐操作,任务多核拆分,流水线的优化技巧等。
本实验内容和代码基于 Neuware 1.6.1 版本。
涉及到的代码,请访问https://github.com/CambriconECO/BANGC_Gemm_Tutorial 获取。
二、HOST端实现
矩阵乘Demo执行过程中,用户先输入参数m,k,n,代表要计算的左右矩阵分别为m*k和k*n大小,HOST端对这两个矩阵进行随机赋值,将输入矩阵以及大小相应的参数传入MLU端进行矩阵运算,最后将运算结果传回HOST端,在HOST端打印矩阵乘的硬件处理时间。
HOST端关键代码如下:
1)输入左右矩阵初始化
float *A = (float *)malloc(M * K * sizeof(float));
float *B = (float *)malloc(K * N * sizeof(float));
float *C = (float *)malloc(M * N * sizeof(float));
float *Cmlu = (float *)malloc(M * N * sizeof(float));
// 给A和B矩阵随机赋值
for (int i = 0; i < M; i++)
{
for (int j = 0; j < K; j++)
{
A[i*K +j] = (i + rand()%16)/217.0;
}
}
int p = 0;
for (int i = 0; i < K; i++)
{
for (int j = 0; j < N; j++)
{
B[i*N +j] = ((float)(rand()%20+3))/1003.0;
}
}
2)准备相关参数,启动Kernel,将参数传入MLU端
cnrtDim3_t dim;cnrtFunctionType_t func_type = CNRT_FUNC_TYPE_BLOCK;
dim.x = 1;dim.y = 1;dim.z = 1;CNRT_CHECK(cnrtMalloc((void **)&d_c, sizeof(half) * M * N_align));CNRT_CHECK(cnrtMalloc((void **)&d_a, sizeof(half) * M * K));CNRT_CHECK(cnrtMalloc((void **)&d_w, sizeof(half) * K * N_align)); A_half = (half *)malloc(sizeof(half) * M * K);B_half = (half *)malloc(sizeof(half) * K * N_align);cnrtKernelInitParam_t init_param;CNRT_CHECK(cnrtCreateKernelInitParam(&init_param));CNRT_CHECK(cnrtInitKernelMemory((const void*)gemm16Kernel, init_param));cnrtKernelParamsBuffer_t params;CNRT_CHECK(cnrtGetKernelParamsBuffer(¶ms)); CNRT_CHECK(cnrtKernelParamsBufferAddParam(params, &d_c, sizeof(half *))); CNRT_CHECK(cnrtKernelParamsBufferAddParam(params, &d_a, sizeof(half *)));CNRT_CHECK(cnrtKernelParamsBufferAddParam(params, &d_w, sizeof(half *)));CNRT_CHECK(cnrtKernelParamsBufferAddParam(params, &M, sizeof(uint32_t)));CNRT_CHECK(cnrtKernelParamsBufferAddParam(params, &K, sizeof(uint32_t)));CNRT_CHECK(cnrtKernelParamsBufferAddParam(params, &N_align, sizeof(uint32_t)));cnrtNotifier_t notifier_start; // A pointer which points to the struct describing notifier.cnrtNotifier_t notifier_end;CNRT_CHECK(cnrtCreateNotifier(¬ifier_start));CNRT_CHECK(cnrtCreateNotifier(¬ifier_end));float timeTotal = 0.0;//printf("start invoke : \n");gettimeofday(&start, NULL);CNRT_CHECK(cnrtPlaceNotifier(notifier_start, pQueue)); // Places a notifier in specified queueCNRT_CHECK(cnrtInvokeKernel_V3((void *)&gemm16Kernel,init_param, dim, params, func_type, pQueue, NULL)); // Invokes a kernel written in Bang with given params on MLUCNRT_CHECK(cnrtPlaceNotifier(notifier_end, pQueue)); // Places a notifier in specified queue
在后续优化的过程中,HOST端的代码基本不变,我们重点关注MLU端代码的开发和优化过程。
三、MLU端实现
MLU端的BANG C实现,我们分成6个步骤,逐一优化,希望帮助大家理解BANG C的使用和优化方法。
1. 直接在GDRAM上使用循环和标量操作进行计算
无须对输入的矩阵作任何处理,使用矩阵乘公式直接计算,完全没有利用到MLU硬件架构的优势,所以整个计算时间很长。MLU端关键代码如下:
#include "mlu.h"__mlu_entry__ void gemm16Kernel(half *outputDDR, half *input1DDR, half *input2DDR, uint32_t m, uint32_t k, uint32_t n) { half ret; __bang_printf("m=%d,k=%d,n=%d\n",m,k,n); for (uint32_t i = 0; i < m; i++) { for (uint32_t j = 0; j < n; j++) { ret = 0; for (uint32_t t = 0; t < k; t++) { ret += input1DDR[i*k+t] * input2DDR[t*n+j]; } outputDDR[i*n+j] = ret; } }}
2. 基本的数据调度
第二步是在第一步的基础上引入NRAM/WRAM的使用,每个core都有自己的NRAM和WRAM,虽然相比于GDRAM空间小,但是可以获得更高的读写带宽和更低的访问时延。(片上存储层次相关介绍可参考BANG C开发者手册)
我们将输入的左右矩阵从GDRAM拷入NRAM中,在NRAM中进行计算,然后拷回GDRAM。需要注意的是,在这个例子中我们假设输入的左右矩阵规模都为256*256,来保证输入的矩阵可以一次性拷入NRAM/WRAM。一旦输入矩阵规模超过NRAM/WRAM的空间大小时,则需要对NRAM/WRAM复用,进行多次拷入和拷出。
MLU端关键代码如下:
#include "mlu.h"__mlu_entry__ void gemm16Kernel(half *outputDDR, half *input1DDR, half *input2DDR, uint32_t m, uint32_t k, uint32_t n) { __nram__ half input1NRAM[256*256]; __nram__ half input2NRAM[256*256]; __nram__ half outputNRAM[256*256]; __memcpy(input1NRAM, input1DDR, m * k * sizeof(half), GDRAM2NRAM); //从 GDRAM拷入NRAM __memcpy(input2NRAM, input2DDR, k * n * sizeof(half), GDRAM2NRAM); for (uint32_t i = 0; i < m; i++) { for (uint32_t j = 0; j < n; j++) { half ret = 0.0; half c = 0.0; for (uint32_t t = 0; t < k; t++) { half v = input1NRAM[i*k+t] * input2NRAM[t*n+j]; half y = v - c; half temp = ret + y; c = ( temp - ret) - y; ret = temp; } outputNRAM[i*n+j] = ret; } } __memcpy(outputDDR, outputNRAM, m * n * sizeof(half), NRAM2GDRAM); //将计算结果拷回GDRAM}
3. 计算的向量化
第三步在以上的基础上,使用BANG C提供的向量计算指令完成矩阵乘的计算,采用向量计算指令可以更好地发挥MLU硬件性能,减少计算时间。
我们先介绍下后续要解决的矩阵乘中的矩阵规模大小问题,为了方便展示和读者理解,假设的是左矩阵规模大小为256*256,右矩阵规模大小为256*N(N可被256整除)。

在这种情况下,输入的左矩阵可一次性拷入NRAM,在执行卷积指令操作时,将输入的右矩阵拷入WRAM中。在往WRAM拷入前,需要对数据进行量化处理,并且摆放成特定要求的数据摆放格式,使用__bang_conv指令进行计算。由于右矩阵规模较大,将右矩阵分批次拷入WRAM进行计算。
MLU端关键代码如下。其中,all_round表示计算的循环次数,这和右矩阵规模大小相关;dst_stride和src_stride代表调整右矩阵数据摆放格式过程中的步长;total_times表示调整右矩阵数据格式的次数,因为目前MLU270上有64个卷积计算单元,所以需要将原本顺序摆放的数据按照64个为一组间隔摆放。
#include "mlu.h"
#define ROUND 256
__mlu_entry__ void gemm16Kernel(half *outputDDR, int8_t *input1DDR, int8_t *input2DDR,
uint32_t m, uint32_t k, uint32_t n, int16_t pos) {
__nram__ int8_t input1NRAM[256*256];
__nram__ int8_t input2NRAM[256*256];
__nram__ int8_t input2NRAM_tmp[256*256];
__wram__ int8_t input2WRAM[256*256];
__nram__ half outputNRAM[256*256];
__memcpy(input1NRAM, input1DDR, m * k * sizeof(int8_t), GDRAM2NRAM);
//在这里将左矩阵一次性拷入NRAM
int all_round = n / ROUND;
int32_t dst_stride = (ROUND * k / 64) * sizeof(int8_t);
int32_t src_stride = k * sizeof(int8_t);
int32_t size = k * sizeof(int8_t);
int32_t total_times = ROUND / 64;
//__bang_printf("taskDim=%d,clusterId=%d,coreId=%d\n",taskDim,clusterId,coreId);
for(int i = 0; i < all_round; i++) {
__bang_write_zero((half *)input2NRAM_tmp, 256 * 128);
__bang_write_zero((half *)input2NRAM, 256 * 128);
__memcpy(input2NRAM_tmp, input2DDR + i * ROUND * k,
k * ROUND * sizeof(int8_t), GDRAM2NRAM);
for (int j = 0; j < total_times; j++) { //这里将数据摆放成bang_conv可以使用的格式
__memcpy(input2NRAM + j * k, input2NRAM_tmp + j * 64 * k,
size, NRAM2NRAM, dst_stride, src_stride, 64);
}
__memcpy(input2WRAM, input2NRAM, ROUND*k*sizeof(int8_t), NRAM2WRAM);
__bang_conv(outputNRAM, input1NRAM, input2WRAM, k, m, 1, 1, 1, 1, 1, ROUND, pos);
__memcpy(outputDDR + i * ROUND,
outputNRAM,
ROUND * sizeof(half),
NRAM2GDRAM,
n * sizeof(half),
ROUND * sizeof(half),
m-1);
/*for (int j = 0; j < m; j++) { //要对每轮计算的结果进行拼接
__memcpy(outputDDR + i * ROUND + j * n, outputNRAM + j * ROUND,
ROUND * sizeof(half), NRAM2GDRAM);
}*/
}
}
4. 计算任务的多核拆分
在第三步的计算中,我们只使用了1个MLU core进行计算,MLU270上有16个MLU core,这一步可以进一步采用16个core并行运算。根据输入矩阵规模的大小,将输入矩阵拆分成多份并分配给不同的计算core,最后再对计算结果进行合并,提高了计算效率。
MLU端关键代码如下。在实现过程中,我们会用到与并行相关的内置变量:taskDim表示任务规模,taskId表示程序运行时所分配的任务ID,在这步的方法中taskDim=16,taskId范围为[0,15]。更多关于taskDim和taskId的介绍,读者可以参考BANG C用户手册第5章的内容:
#include "mlu.h"
#define ROUND 256
#define NRAM_ARRAY_SIZE 256*256
__mlu_entry__ void gemm16Kernel(half *outputDDR, int8_t *input1DDR, int8_t *input2DDR,
uint32_t m, uint32_t k, uint32_t n, int16_t pos) {
__nram__ int8_t input1NRAM[NRAM_ARRAY_SIZE];
__nram__ int8_t input2NRAM[NRAM_ARRAY_SIZE];
__nram__ int8_t input2NRAM_tmp[NRAM_ARRAY_SIZE];
__wram__ int8_t input2WRAM[NRAM_ARRAY_SIZE];
__nram__ half outputNRAM[NRAM_ARRAY_SIZE];
__memcpy(input1NRAM, input1DDR, m * k * sizeof(int8_t), GDRAM2NRAM);
//在这里将左矩阵一次性拷入NRAM
int all_round = n / ( taskDim * ROUND); //因为现在使用16个核同时运算,所以每个核循环的次数也相应减少
int32_t dst_stride = (ROUND * k / 64) * sizeof(int8_t);
int32_t src_stride = k * sizeof(int8_t);
int32_t size = k * sizeof(int8_t);
int32_t total_times = ROUND / 64;
//__bang_printf("taskDim=%d,taskId=%d\n",taskDim, taskId);
for(int i = 0; i < all_round; i++) {
__memcpy(input2NRAM_tmp, input2DDR + ROUND * (i * taskDim + taskId) * k , //只涉及这个核需要的数据
k * ROUND * sizeof(int8_t), GDRAM2NRAM);
for (int j = 0; j < total_times; j++) {
__memcpy(input2NRAM + j * k, input2NRAM_tmp + j * 64 * k,
size, NRAM2NRAM, dst_stride, src_stride, 64 - 1);
}
__memcpy(input2WRAM, input2NRAM, ROUND*k*sizeof(int8_t), NRAM2WRAM);
__bang_conv(outputNRAM, input1NRAM, input2WRAM, k, m, 1, 1, 1, 1, 1, ROUND, pos);
for (int j = 0; j < m; j++) { //向GDRAM回写的时候也要注意每个核的位置不同
__memcpy(outputDDR + (i * taskDim + taskId) * ROUND + j * n,
outputNRAM + j * ROUND, ROUND * sizeof(half), NRAM2GDRAM);
}
}
}
5. SRAM的使用
第五步是在第四步的基础上引入Shared-RAM,在MLU270中,一个cluster中的4个core共享一个SRAM。在第四步中,因为使用了4个cluster的16个core进行并行计算,而同1个cluster上的4个core在从GDRAM上拷贝数据到各自的NRAM/WRAM时,会争抢这个cluster到GDRAM的带宽,从而导致数据读取速度降低。所以我们将数据先从GDRAM拷贝到SRAM,再从SRAM分发到NRAM/WRAM中,避免了调度争抢问题,提高了数据读取速度。
特别注意的是,从GDRAM拷入数据到SRAM和从SRAM拷入数据到NRAM这两个操作,是由两种不同功能的core执行(这个会在后文中解释),所以这两个操作是并行的关系。为了避免数据冲突,我们要设置同步功能,保证数据从GDRAM拷入到SRAM之后,才能执行从SRAM拷入到NRAM的过程,在BANG C中我们可以使用内置的__sync_cluster()函数完成同步功能。图示如下:

整个执行过程如下图所示:

MLU端关键代码如下,其中clusterId表示此时执行任务的是哪个cluster,范围为[0,3]:
#include "mlu.h"
#define ROUND 256
__mlu_entry__ void gemm16Kernel(half *outputDDR, int8_t *input1DDR, int8_t *input2DDR,
uint32_t m, uint32_t k, uint32_t n, int16_t pos) {
__nram__ int8_t input1NRAM[256*256];
__nram__ int8_t input2NRAM[256*256];
__nram__ int8_t input2NRAM_tmp[256*256];
__wram__ int8_t input2WRAM[256*256];
__nram__ half outputNRAM[256*256];
__memcpy(input1NRAM, input1DDR, m * k * sizeof(int8_t), GDRAM2NRAM);
//在这里将左矩阵一次性拷入NRAM
int all_round = n / ( taskDim * ROUND); //因为现在使用16个核同时运算,所以每个核循环的次数也相应减少
int32_t dst_stride = (ROUND * k / 64) * sizeof(int8_t);
int32_t src_stride = k * sizeof(int8_t);
int32_t size = k * sizeof(int8_t);
int32_t total_times = ROUND / 64;
__mlu_shared__ int8_t input2SRAM[256*1024];
//_bang_printf("taskDim=%d,clusterId=%d,coreId=%d\n",taskDim,clusterId,coreId);
for(int i = 0; i < all_round; i++)
{
// copy GDRAM2SRAM
__memcpy(input2SRAM, input2DDR + ROUND * (i * taskDim + clusterId * 4) * k ,
k * ROUND * 4 * sizeof(int8_t), GDRAM2SRAM); // 只将右矩阵拷入SRAM中
__sync_cluster(); //设置sync barrier
// copy SRAM2NRAM
__memcpy(input2NRAM_tmp, input2SRAM + ROUND * coreId * k , k * ROUND * sizeof(int8_t), SRAM2NRAM);
// 将数据摆好对应的格式
for (int j = 0; j < total_times; j++) {
__memcpy(input2NRAM + j * k, input2NRAM_tmp + j * 64 * k,
size, NRAM2NRAM, dst_stride, src_stride, 64 - 1);
}
// copy NRAM2WRAM
__memcpy(input2WRAM, input2NRAM, ROUND*k*sizeof(int8_t), NRAM2WRAM);
// compute
__bang_conv(outputNRAM, input1NRAM, input2WRAM, k, m, 1, 1, 1, 1, 1, ROUND, pos);
// copy NRAM2GDRAM
for (int j = 0; j < m; j++) { //向GDRAM回写的时候也要注意每个核的位置不同
__memcpy(outputDDR + (i * taskDim + taskId) * ROUND + j * n,
outputNRAM + j * ROUND, ROUND * sizeof(half), NRAM2GDRAM);
}
__sync_cluster(); //设置sync barrier
}
}
6. 基本的流水优化
MLU270上,每个cluster除了4个普通的计算core之外,还有专门用以管理片上总线和SRAM的memory core。这就是上一步提到的两种不同功能的计算单元,为我们使用流水线优化创造了条件。
第六步在上面的基础上,实现了4个cluster并行计算,且每个cluster中的memory core和其他4个 MLU core构成流水线的计算模式。在每个cluster中,memory core只负责将数据从GDRAM拷入SRAM,其余的每个MLU core则负责从SRAM拷入数据、矩阵乘计算、将数据拷回GDRAM。
我们设置了在SRAM上的两个变量input2SRAM1,input2SRAM2。初始时,memory core从GDRAM上拷入数据到input2SRAM1,当数据拷入完成后,4个core开始工作,它们将自己需要的数据部分从input2SRAM1拷入进行计算。在MLU core工作的同时,memory core不会停止工作,它会将下一次需要计算的数据从GDRAM拷入input2SRAM2,供给4个MLU core在下一次使用,减少了拷入等待时间,input2SRAM1和input2SRAM2交替读写重复上述过程直至所有数据计算完成。
从中可以发现,耗时很长GDRAM到SRAM的这一步拷贝时间被“藏起来”了。和原来相比,在相同的时间内,我们搬运了更多的GDRAM数据到片上并且完成了计算。那么为什么会使用两个SRAM变量对GDRAM上的数据进行拷贝呢?因为在上述过程中,MLU core在从SRAM读取数据的同时,SRAM也会从GDRAM写入数据,如果只使用一个SRAM变量,则很有可能导致MLU core应该读取的数据在读取前被写入覆盖。
有经验的开发者可能已经发现,这里使用的是一种常用的数据流控制的处理技巧,乒乓操作。
整个过程如下图所示:

MLU端关键代码如下:
#include "mlu.h"
#define ROUND 256
__mlu_entry__ void gemm16Kernel(half *outputDDR, int8_t *input1DDR, int8_t *input2DDR,
uint32_t m, uint32_t k, uint32_t n, int16_t pos) {
__nram__ int8_t input1NRAM[256*256];
__nram__ int8_t input2NRAM[256*256];
__nram__ int8_t input2NRAM_tmp[256*256];
__wram__ int8_t input2WRAM[256*256];
__nram__ half outputNRAM[256*256];
__memcpy(input1NRAM, input1DDR, m * k * sizeof(int8_t), GDRAM2NRAM);
//在这里将左矩阵一次性拷入NRAM
int all_round = n / ( taskDim * ROUND); //因为现在使用16个核同时运算,所以每个核循环的次数也相应减少
int32_t dst_stride = (ROUND * k / 64) * sizeof(int8_t);
int32_t src_stride = k * sizeof(int8_t);
int32_t size = k * sizeof(int8_t);
int32_t total_times = ROUND / 64;
__mlu_shared__ int8_t input2SRAM1[256*1024];
__mlu_shared__ int8_t input2SRAM2[256*1024];
__mlu_shared__ int8_t * input2SRAM_read;
__mlu_shared__ int8_t * input2SRAM_write;
input2SRAM_write=input2SRAM1;
// copy GDRAM2SRAM
__memcpy(input2SRAM_write, input2DDR + ROUND * (clusterId * 4) * k,
k * ROUND * 4 * sizeof(int8_t), GDRAM2SRAM); // 只将右矩阵拷入SRAM中
__sync_cluster(); //设置sync barrier
//_bang_printf("taskDim=%d,clusterId=%d,coreId=%d\n",taskDim,clusterId,coreId);
for(int i = 0; i < all_round-1; i++)
{
if (i % 2 == 0)
{
input2SRAM_read=input2SRAM1;
input2SRAM_write=input2SRAM2;
} else {
input2SRAM_read=input2SRAM2;
input2SRAM_write=input2SRAM1;
}
if (coreId == 0x80) {
// copy GDRAM2SRAM
__memcpy(input2SRAM_write, input2DDR + ROUND * ((i+1) * taskDim + clusterId * 4) * k,
k * ROUND * 4 * sizeof(int8_t), GDRAM2SRAM); // 只将右矩阵拷入SRAM中
} else {
// copy SRAM2NRAM
__memcpy(input2NRAM_tmp, input2SRAM_read + ROUND * coreId * k , k * ROUND * sizeof(int8_t), SRAM2NRAM);
// 将数据摆好对应的格式
for (int j = 0; j < total_times; j++) {
__memcpy(input2NRAM + j * k, input2NRAM_tmp + j * 64 * k,
size, NRAM2NRAM, dst_stride, src_stride, 64 - 1);
}
// copy NRAM2WRAM
__memcpy(input2WRAM, input2NRAM, ROUND*k*sizeof(int8_t), NRAM2WRAM);
// compute
__bang_conv(outputNRAM, input1NRAM, input2WRAM, k, m, 1, 1, 1, 1, 1, ROUND, pos);
// copy NRAM2GDRAM
for (int j = 0; j < m; j++) { //向GDRAM回写的时候也要注意每个核的位置不同
__memcpy(outputDDR + (i * taskDim + taskId) * ROUND + j * n,
outputNRAM + j * ROUND, ROUND * sizeof(half), NRAM2GDRAM);
}
}
__sync_cluster(); //设置sync barrier
}
__memcpy(input2NRAM_tmp, input2SRAM_write + ROUND * coreId * k , k * ROUND * sizeof(int8_t), SRAM2NRAM);
// 将数据摆好对应的格式
for (int j = 0; j < total_times; j++) {
__memcpy(input2NRAM + j * k, input2NRAM_tmp + j * 64 * k,
size, NRAM2NRAM, dst_stride, src_stride, 64 - 1);
}
// copy NRAM2WRAM
__memcpy(input2WRAM, input2NRAM, ROUND*k*sizeof(int8_t), NRAM2WRAM);
// compute
__bang_conv(outputNRAM, input1NRAM, input2WRAM, k, m, 1, 1, 1, 1, 1, ROUND, pos);
// copy NRAM2GDRAM
for (int j = 0; j < m; j++) { //向GDRAM回写的时候也要注意每个核的位置不同
__memcpy(outputDDR + ((all_round - 1) * taskDim + taskId) * ROUND + j * n,
outputNRAM + j * ROUND, ROUND * sizeof(half), NRAM2GDRAM);
}
}
四、性能情况
由于循环操作计算矩阵乘性能太差,计算时间太长,没有实际意义,故不在此向读者展示,下图只罗列出后四步在相同规模下的硬件执行时间的比较。
规模:m=256 k=256 n=327680
|
实现方式 |
耗时 (ms) |
提升幅度 |
|
NRAM+conv+单核 |
83.637 |
- |
|
NRAM+conv+16核 |
14.142 |
491.40% |
|
SRAM+conv+16核 |
13.026 |
8.56% |
|
SRAM+conv+16核+流水 |
12.375 |
5.26% |
五、向量化操作中的数据对齐要求
在以上的所有优化过程中我们为了简化表述,降低理解的的难度,都没有涉及到向量化操作中的数据对齐要求。在本小节中我们专门讨论这个问题。
对于大多数对位向量操作,补齐只要在末尾处补零即可。在本教程中,我们使用一个相对复杂一些的例子,__bang_conv来解释一些对齐的要求和技巧。针对每个函数的对齐要求在BANG C的使用手册中都有描述。例如 __bang_conv,可以看到对齐要求为:
<channal_input> * sizeof(type of input) must be divisible by 64 on MLU220/MLU270;
<channal_output> must be divisible by 64 on MLU220/MLU270;
假设输入规模M,K,N 分别为250, 250,150。对齐的目标位置:
#define PAD_UP(x, y) (x / y + static_cast<int>((x) % y > 0)) * y
#define PAD_DN(x, y) (x / y) * y
PAD_UP向上对齐,PAD_DN表示向下对齐。
uint32_t k_aligned = PAD_UP(k, 128);
uint32_t n_slice = PAD_DN(NRAM_ARRAY_SIZE / k_aligned, 64);
这里k_aligned为对齐到128,结果为256。
n_slice则为K对齐后,每次能拷入NRAM的最大N的数量,同样也要对齐。而这里如果采用向上对齐则会超出NRAM的存储范围,必须向下对齐。
对齐前的效果:

注意这部分代码 __bang_conv(outputNRAM, input1NRAM, input2WRAM, k, m, 1, 1, 1, 1, 1, n, pos);将k映射到了channal_input,n映射到了channal_output。所以在数据上需要对这两个维度进行对齐。
数据类型为int8,所以sizeof(type of input) = 1 ,后面我们就考虑如何将K和N对齐到64的倍数上。
左矩阵的对齐相对简单,只需要考虑K的对齐就可以,具体如下:

代码实现上,使用带步长的__memcpy功能来实现对齐操作。需要注意的是,对于对齐的部分,要利用__bang_write_zero完成数据初始化,避免影响后面的计算结果。
__bang_write_zero(input1NRAM, NRAM_ARRAY_SIZE);
__memcpy(input1NRAM,
input1DDR,
k * sizeof(int8_t),
GDRAM2NRAM,
k_aligned * sizeof(int8_t),
k * sizeof(int8_t),
m-1);
此处k=250,k_aligned=256,m=250
右矩阵的对齐原理则相对复杂,需要向两个方向对齐。

这里的实现方式上相对简单,对齐的关键依旧是K的对齐,N的对齐只要在后面连续补零即可。
对于K的对齐依旧使用带步长的__memcpy功能来实现。
在计算__bang_conv部分依旧使用了固定长度的n,而不是对齐的n,这是因为这部分补0的内容对计算结果没有影响,而且对计算性能没有影响。
__bang_write_zero(temp, NRAM_ARRAY_SIZE);
__memcpy(temp,
input2DDR + offset * k,
k * sizeof(int8_t),
GDRAM2NRAM,
k_aligned * sizeof(int8_t),
k * sizeof(int8_t),
n_aligned-1);
for (int j = 0; j < total_times; j++) {
__memcpy(input2NRAM + j * k_aligned, temp + j * 64 * k_aligned,
size, NRAM2NRAM, dst_stride, src_stride, 64 - 1);
}
__memcpy(input2WRAM, input2NRAM, n_slice*k_aligned*sizeof(int8_t), NRAM2WRAM);
__bang_conv(outputNRAM, input1NRAM, input2WRAM, k_aligned, m, 1, 1, 1, 1, 1, n_slice, pos);
for (int j = 0; j < m; j++) {
__memcpy(outputDDR + offset + j * n,
outputNRAM + j * n_slice,
n_aligned * sizeof(half),
NRAM2GDRAM);
需要注意的是,为了满足对齐的要求程序往往要付出一些额外的性能成本。这些额外的性能成本主要来自于我们为了对K补齐所做的__memcpy with stride。
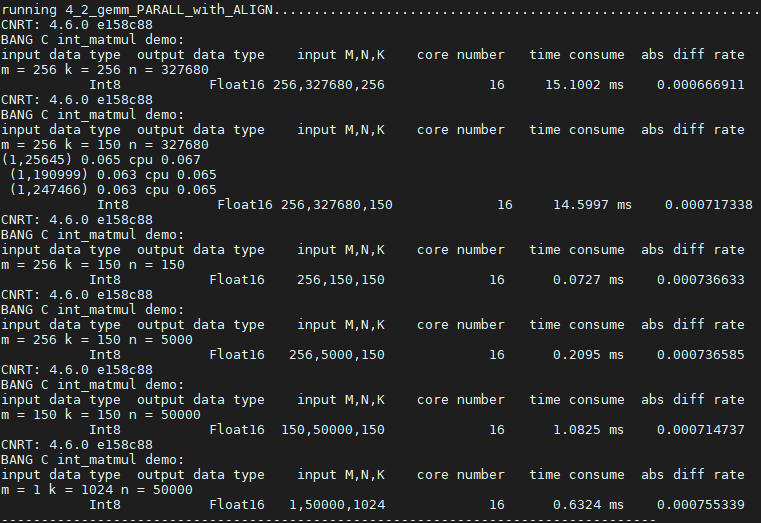
以下是在某些规模上的性能测试数据参考。